An excellent course on machine learning

Following Olli’s recommendation I took a crack at Andrew Ng’s machine learning course on Coursera. It’s for free, it’s well-designed and taught and I highly recommend it. I’d like to share my codes for the course, but I think that would be against the spirit of such an online class.

Some observations:

• It’s an introductory course, so there are no proofs. The focus is on graphical intuition, implementing the algorithms in Octave/Matlab and the practicalities of large-scale machine learning projects.
• The goal is not to accurately estimate the \(\beta\) and the uncertainty around it, but to be precise in predicting the \(\hat{y}\) out of sample. (See also here.)
• The course is refreshingly different from what we normally study and I think best taken not as a substitute, but as a complement to econometrics classes.

• It uses a different vocabulary:

  Machine learning	Econometrics
  example	observation
  (to) learn	(to) estimate
  hypothesis	estimation equation
  feature/input	variable
  output/outcome	dependent variable
  bias	constant/intercept
  bias (yeah, twice 🤔)	bias

• Linear regression is introduced through the cost function and its numerical minimization. Ng shows the analytical solution on the side, but he adds that it would only be useful in a “low-dimensional” problem up to 10,000 or so variables.
• I liked the introduction to neural networks in week 4 and the explanation of them as stacked logical operators.
• Insightful discussion of how to use training and cross-validation set errors plotted against the regularization parameter and against the number of observations to identify whether bias or variance is a problem.
• The video on error analysis made me realize that in my patent project I had spend a very large amount of time thinking about appropriate error metrics, but little time actually inspecting the mis-classified patents.

• In a presentation I once attended, Tom Sargent said:

  A little linear algebra goes a long way.

  Similarly here: Only doing a little clustering, for example, we can compress the file size of this image by a factor of six, but preserve a lot of the information (exercise 7):

  Figure: Image compression with PCA

  

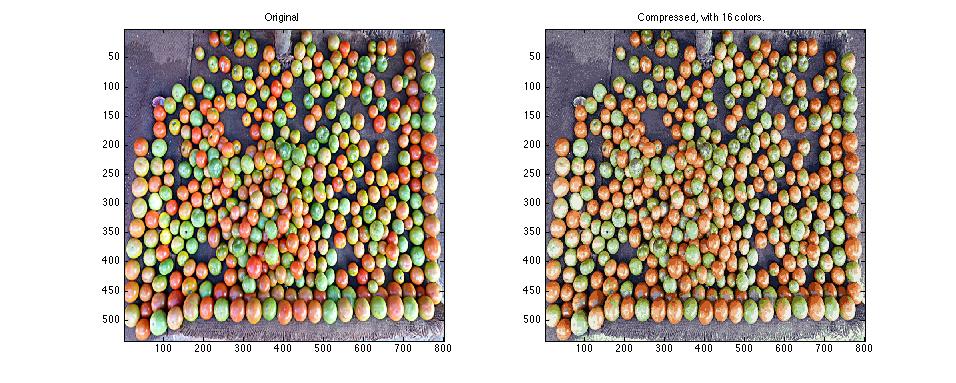
• I hadn’t previously thought of dimension reduction as a debugging method: If you get thousands of features from different sources and you’re not sure if some might be constructed similarly, then dimension reduction weeds out the redundant features.
• Time series data is suspiciously missing from the course.

• He mentions this folk wisdom:

  […] [I]t’s not who has the best algorithm that wins. It’s who has the most data.

• And he recommends asking:

  How much work would it be to get 10x as much data as we currently have?

• Ng stresses again and again that our intuitions on what to optimize often lead us astray. Instead we should plot error curves, do error analysis and look at where the bottlenecks in the machine learning pipepline are.
• I also liked the discussion of using map-reduce for parallelization at the end of the class. Hal Varian also discussed that here.