Phillips curve in the United States

19 Nov 2017

Joseph Gagnon has written a blog post at the Peterson Institute about the Phillips curve in the United States.

Some economists have observed that the employment gap turned positive this year, but inflation has not increased. Gagnon argues that we should not be too quick to infer from this that the Phillips curve relationship has broken down, as high employment may take a while to raise prices. And he adds that this relationship is weaker in low inflation environments due to hesitancies to lower prices (i.e., nominal rigidities).

He kindly provides data and codes at the bottom of his codes, but let’s try to reproduce his figure using only public data from FRED.

In R, first install some packages:

install.packages("tidyverse")
install.packages("zoo")
install.packages("lubridate")
install.packages("ggthemes")
install.packages("devtools")
devtools::install_github("jcizel/FredR")

Load the packages:

library(tidyverse)
library(zoo)
library(lubridate)
library(ggthemes)
library(FredR)

Now get some series on core (no food, no energy) personal consumption expenditures and on the unemployment rate from FRED.

To access data from FRED, you need to register an API key and insert below.

api_key <- "yourkeyhere"
fred    <- FredR(api_key)

mt <- fred$series.observations(series_id = "PCEPILFE") %>%
  mutate(date = as.Date(date)) %>% 
  select(date, pce = value)

mt <- fred$series.observations(series_id = "UNRATE") %>%
  mutate(date = as.Date(date)) %>% 
  select(date, unrate = value) %>% 
  full_join(., mt)

These are monthly series, so aggregate them to quarterly values:

qt <- mt %>% 
  mutate(yq     = as.yearqtr(date),
         pce    = as.numeric(pce),
         unrate = as.numeric(unrate)) %>% 
  group_by(yq) %>% 
  summarize(pce    = mean(pce),
            unrate = mean(unrate))

Download quarterly CBO estimates for the natural rate of unemployment from FRED and calculate the employment gap as current employment rate minus natural rate.

df  <- fred$series.observations(series_id = "NROU") %>%
  mutate(yq = as.yearqtr(paste0(year(date), " Q", quarter(date)))) %>% 
  filter(yq <= "2017 Q4") %>% 
  select(yq, nru = value) %>% 
  mutate(nru = as.numeric(nru)) %>% 
  full_join(qt, nru) %>% 
  mutate(egap = nru - unrate)

Make a plot:

ggplot(df, aes(yq, egap)) +
  geom_hline(yintercept = 0, size = 0.3, color = "grey80") +
  theme_tufte(base_family="Helvetica", ticks=FALSE) +
  geom_line() +
  labs(title    = "US employment gaps",
       subtitle = "1949Q1–2017Q4",
       x        = "Employment gap",
       y        = "Quarters")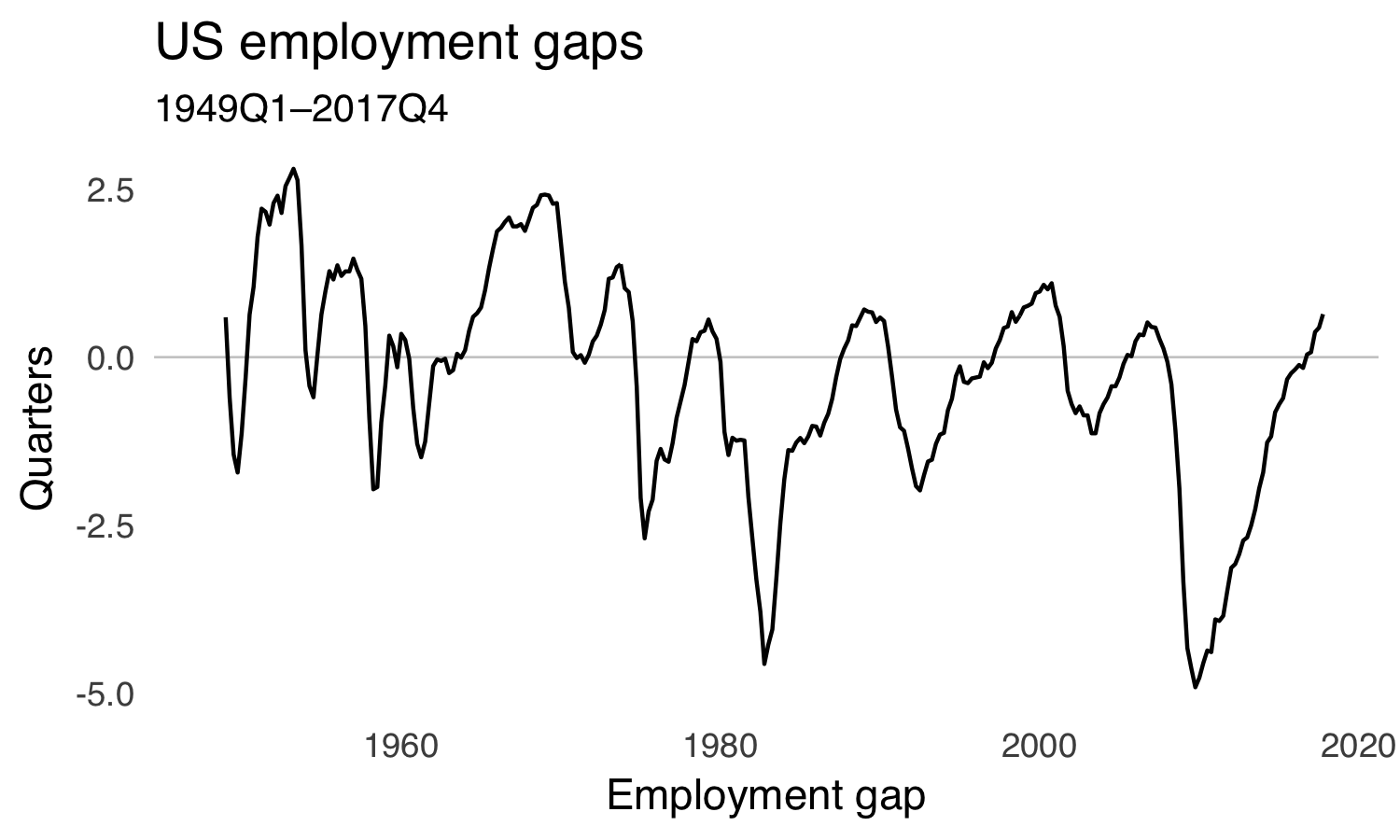

Employment gap in the United States, 1949-2017

We see that the employment gap was negative for a long time after the financial crisis but has recently turned positive. That’s the bit of data that Gagnon and others are arguing about.

Now we create the variables that Gagnon uses. We lag the employment gap by four quarters and calculate the inflation rate as the year-on-year change in the price level:

df <- df %>% 
  mutate(egap_l = dplyr::lag(egap, 4),
         cpi = 100*(pce - dplyr::lag(pce, 4)) / dplyr::lag(pce, 4))

Take the moving average of the last three years and detrend the inflation rate to get the “change in inflation”:

df <- df %>% 
  ungroup() %>% 
  mutate(cpi_ma = 
           rollapply(cpi, width=12, FUN=function(x) mean(x, na.rm=TRUE), 
                     by=1, by.column=TRUE, partial=TRUE, fill=NA, align="right"),
         cpi_ma = ifelse(is.nan(cpi_ma), NA, cpi_ma),
         cpi_change = cpi - cpi_ma)

Last, we check in which periods inflation (four quarters before) was above three percent. And we truncate the data to the same sample as in Gagnon’s analysis.

df <- df %>% 
  mutate(cpi_l = dplyr::lag(cpi, 4)) %>% 
  mutate(high_inflation = (cpi_l >= 3))

df <- df %>% 
  filter((yq >= "1963 Q1") & (yq <= "2017 Q3"))

Now we can reproduce the scatterplots:

ggplot(df, aes(egap_l, cpi_change, color = high_inflation, 
               shape = high_inflation)) +
  geom_hline(yintercept = 0, size = 0.3, color = "grey50", linetype = "dotted") +
  geom_vline(xintercept = 0, size = 0.3, color = "grey50", linetype = "dotted") +
  geom_point(alpha = 0.5, stroke = 0, size = 3) +
  theme_tufte(base_family="Helvetica", ticks=FALSE) +
  geom_smooth(method = "lm", se = FALSE, size = 0.4, show.legend = FALSE) +
  labs(title    = "US Phillips curves with low and high inflation",
       subtitle = "1963Q1–2017Q3",
       caption  = "Source: FRED and own calculations following\nGagnon (2017) \"There Is No Inflation Puzzle\".",
       x        = "employment gap",
       y        = "change in inflation") +
  geom_text(data=subset(df, yq == "2017 Q3"),
            aes(egap_l, cpi_change, label=yq), vjust = -10, hjust = 2,
            show.legend = FALSE) +
  geom_segment(aes(x = -1.2, xend=df$egap_l[df$yq == "2017 Q3"], 
                   y = 1.85, yend=df$cpi_change[df$yq == "2017 Q3"]), 
               arrow = arrow(length = unit(0.1, "cm")),
               show.legend = FALSE) +
  scale_colour_manual(name = "Inflation:",
                      labels = c("< 3%", "> 3%"),
                      values = c("#F8766D", "#00BFC4")) +
  scale_shape_manual(name = "Inflation:",
                     labels = c("< 3%", "> 3%"),
                     values = c(17, 19))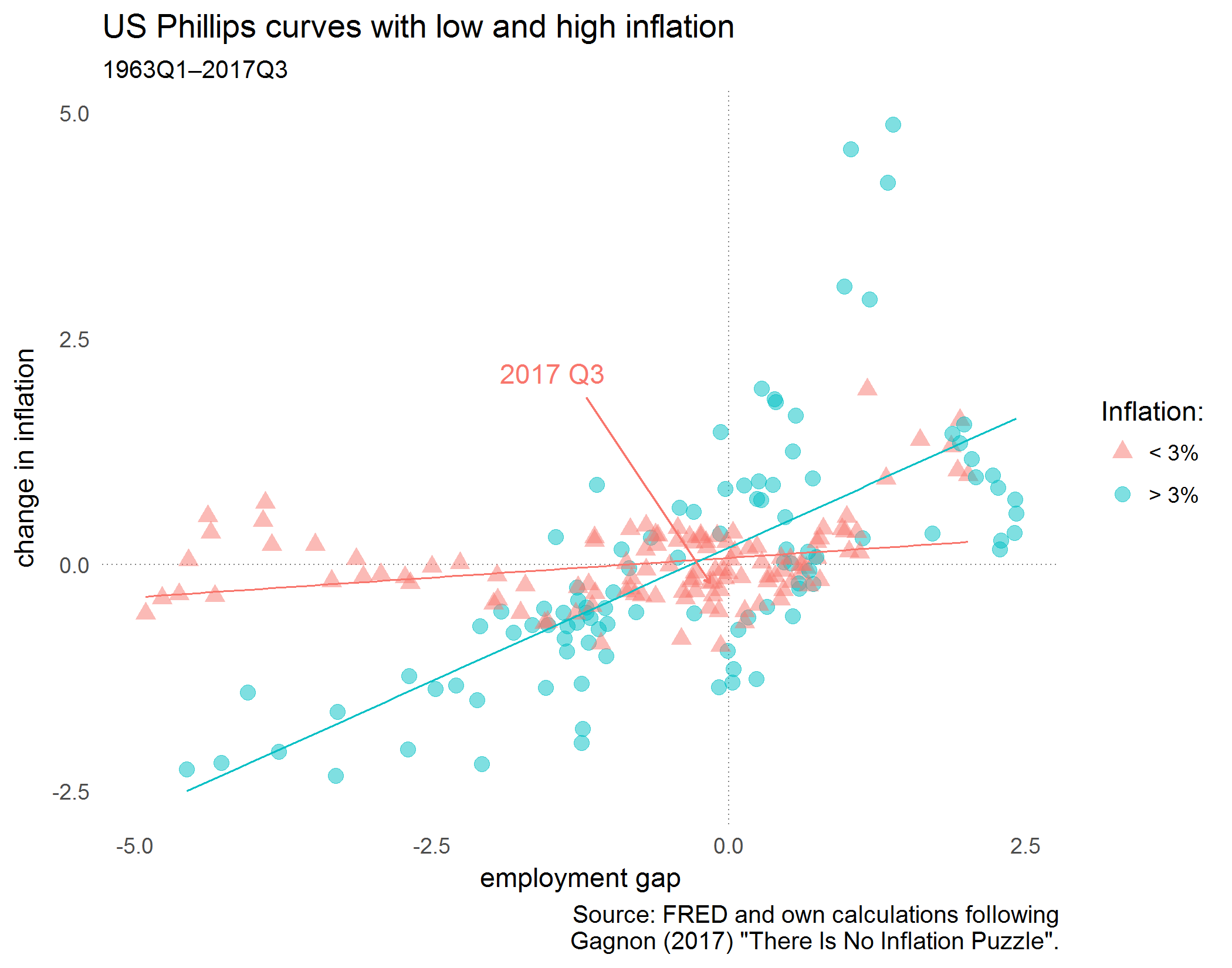

US Phillips curves with low and high inflation 1963-2017

We see indeed that there’s a relationship, but it’s more pronounced in the high inflation regime. And the most recent datapoint “2017 Q3” shows that – a year ago – the employment gap was still slighty negative with -0.16 and the change in inflation in 2017 Q3 was also negative with -0.20.